| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 유니티 3D
- 정처기 필기
- 퐁
- 게임
- 정처기
- 프로그래머스 #최소힙 #우선순위 큐
- portal
- 필기
- 게임 개발
- 유니티
- Unity2D
- Vampire Survivors
- Unity #Unity2D #Portal
- Pong
- 1인 게임 제작
- 합격
- 1인 게임
- 게임 제작
- 1인 게임 개발
- 정보처리기사
- unity3d
- Unity
- FPS
- 유니티3d
- 1인 개발
- 게임제작
- 토이 프로젝트
- 자바스크립트
- 3회차
- 자바스크립트 게임
- Today
- Total
Coding Feature.
백준) 16937번: 두 스티커 in C 본문

16937번: 두 스티커
첫째 줄에 모눈종이의 크기 H, W, 둘째 줄에 스티커의 수 N이 주어진다. 다음 N개의 줄에는 스티커의 크기 Ri, Ci가 주어진다.
www.acmicpc.net
Solution
이 문제는 모든 경우의 수를 어떻게 분기점을 잡고 나눌 지, if 문을 어떻게 작성할 지가 관건이다.
모눈종이와 두 스티커 모두 직사각형이고 격자선과 일치하게끔 붙이기 때문에 결국 다음과 같이 생각해낼 수 있었다.
어쨌든 모눈종이에 최대한 들어가게 두 스티커를 붙이기 위해서는 두 스티커를 접하게끔 붙이는 것이 맞고,
접하는 것도 두 스티커의 한 꼭짓점이 닿게끔 붙이는 것이 더 나을 것이다.
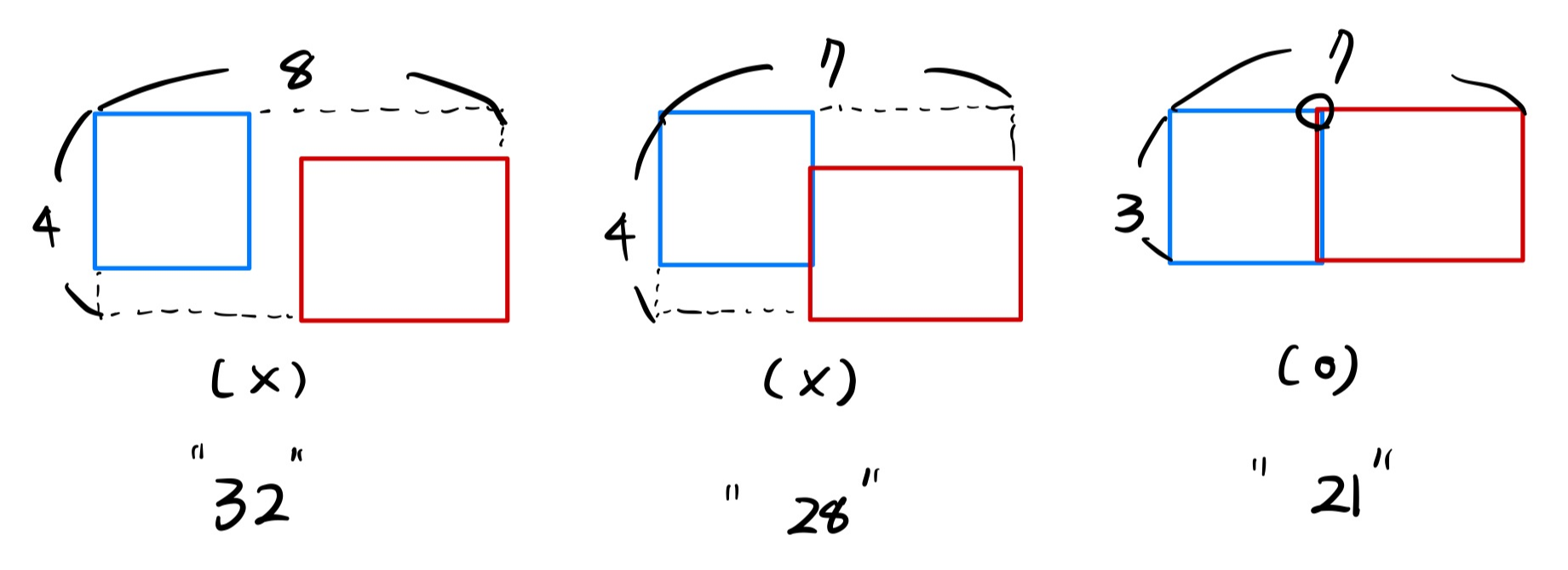
그러면 두 스티커의 한 꼭짓점이 닿은체 접하게끔 붙이는 모든 경우의 수를 고려해보아야 한다.
어떤 두 스티커의 양 변 길이를 각각 (X1, Y1), 그리고 (X2, Y2)라고 하자. 이미 문제 조건으로 스티커를 90도로 회전하는 것도 가능하다고 나와 있었다.
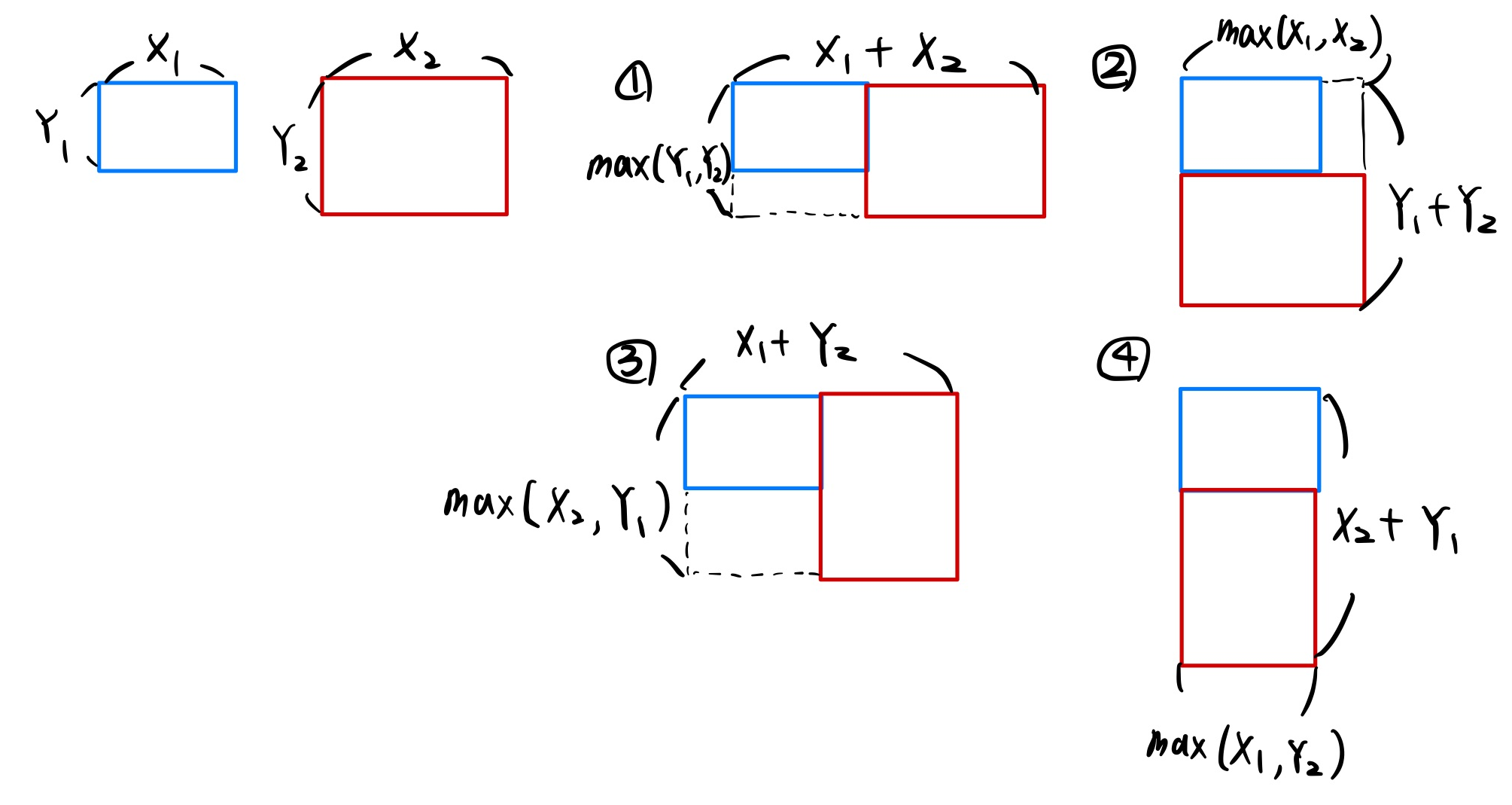
그러면 두 스티커를 붙이는 데 필요한 공간의 크기는 다음과 같이 4가지 경우로 나뉘는 것을 알 수 있다.
1) X1+X2, max(Y1, Y2)
2) Y1+Y2, max(X1, X2)
3) X1+Y2, max(X2, Y1)
4) X2+Y1, max(X1, Y2)
그림을 보면 더 이해가 쉬울 것이다.
그리고 위 4 가지 경우에 대해서 각 변의 길이가 H, W인 모눈종이에 들어가는지 확인을 해야 한다. (H, W) 그리고 (W, H)로 번갈아가면서 비교를 해야 한다.
그러면 총 2 *4 로 8가지의 경우를 조건문을 통해 비교를 하고, 가능한 경우 두 스티커의 넓이의 합을 가장 큰 값으로 업데이트 해주면서 결과값을 반환해주면 된다.
Code
#include <stdio.h>
void update(int *total, int val){
*total = (*total < val)? val : *total;
};
int max(int A, int B){
return (A > B)? A : B;
};
int check_if_fit(int H, int W, int X1, int Y1, int X2, int Y2){
if( (X1 + X2 <= H && max(Y1, Y2) <= W) || (X1 + X2 <= W && max(Y1, Y2) <= H) )
return 1;
if( (Y1 + Y2 <= H && max(X1, X2) <= W) || (Y1 + Y2 <= W && max(X1, X2) <= H) )
return 1;
if( (X1 + Y2 <= H && max(Y1, X2) <= W) || (X1 + Y2 <= W && max(Y1, X2) <= H) )
return 1;
if( (Y1 + X2 <= H && max(X1, Y2) <= W) || (Y1 + X2 <= W && max(X1, Y2) <= H) )
return 1;
return 0;
};
int main(){
int H, W, N, i, j, total = 0, sum;
int RC[100][2];
scanf("%d %d", &H, &W);
scanf("%d", &N);
for(i=0;i<N;i++)
scanf("%d %d", &RC[i][0], &RC[i][1]);
for(i=0;i<N;i++){
for(j=i+1;j<N;j++){
sum = RC[i][0] * RC[i][1] + RC[j][0] * RC[j][1];
if(check_if_fit(H, W, RC[i][0], RC[i][1], RC[j][0], RC[j][1]))
update(&total, sum);
}
}
printf("%d\n", total);
return 0;
}'코딩테스트 > 백준 solved.ac' 카테고리의 다른 글
| 백준) 16236번: 아기 상어 in C (0) | 2023.07.29 |
|---|---|
| 백준) 1913번: 달팽이 in C (0) | 2023.07.28 |
| 백준) 1695번: 팰린드롬 만들기 in C (0) | 2023.07.27 |
| 백준) 1697번: 숨바꼭질 in C (0) | 2023.07.26 |
| 백준) 16938번: 캠프 준비 in C (0) | 2023.07.23 |




